[x_j^{(k+1)} = arg min_{x_j} f(x_1^{(k+1)}, dots, x_{j-1}^{(k+1)}, x_j, x_{j+1}^{(k)}, dots, x_n^{(k)}) ]

每次固定(x_j)之外的所有变量，对(x_j)进行最小化，然后不断的迭代(x_j)

推导过程

我们就以上述提到的函数来推导一下，加深对这个过程的理解$$f(x,y)=3x^2+5xy+10y2$$

1）首先先寻找一个点，((1,1))，计算此时的函数值

[f(1,1)=3x^2+5xy+10y^2=18 ]

2）分别对x,y求偏导

对x求偏导，并且令其导数为0：

[frac {partial f}{partial x}=6x+5y=0，x=-frac{5}{6}y ]

同理对y求偏导

[frac {partial f}{partial y}=5x+20y=0，y=-frac{1}{4}x ]

3）开始迭代，第一轮

调整x，固定y

[x=-frac{5}{6}y=-frac{5}{6}·1 = -frac{5}{6} ]

调整y，固定x

[y=-frac{1}{4}x=-frac{1}{4}·-frac{5}{6}=frac{5}{24} ]

此时函数值为：

[f(-frac{5}{6},frac{5}{24})=3x^2+5xy+10y^2 approx 2.3438 ]

第一轮结束：

• 函数最小值(f(x,y)=2.3438)
• (|Δx|=|-frac{5}{6}-1| approx 1.8333)
• (|Δy|=|frac{5}{24}-1| approx 0.7917)

4）第二轮

重复第一轮的操作

调整x，固定y

[x=-frac{5}{6}y=-frac{5}{6}·frac{5}{24} = -frac{25}{144} ]

此时函数值为：

[f(-frac{25}{144},frac{5}{24})=3x^2+5xy+10y^2 approx 0.4883 ]

调整y，固定x

[y=-frac{1}{4}x=-frac{1}{4}·-frac{25}{144}=frac{25}{576} ]

此时函数值为：

[f(-frac{25}{144},frac{25}{576})=3x^2+5xy+10y^2 approx 0.1221 ]

第二轮结束：

• 函数最小值(f(x,y)=0.1221)
• (|Δx|=|-frac{25}{6}-(-frac{5}{6})| approx 0.6597)
• (|Δy|=|frac{25}{576}-frac{5}{24}| approx 0.1649)

5）不断的迭代，直至收敛

随着迭代次数的不断增加，(|Δx|)、(Δy)、(f(x,y))都在不断减小

当(|Δx|)、(Δy)均小于(10^{-4})，可以认为函数收敛

凸函数

通过上述的过程模拟，可以找到函数最小值时x,y分别是多少

对于函数(f(x,y)=3x^2+5xy+10y^2)，可以直接计算偏导数为0，从而求出最小值

[frac {partial f}{partial x}=6x+5y=0，x=-frac{5}{6}y ]

[frac {partial f}{partial y}=5x+20y=0，y=-frac{1}{4}x ]

解方程组：

[begin{cases} x=-frac{5}{6}y \ y=-frac{1}{4}x end{cases} ]

[begin{cases} x=0 \ y=0 end{cases} ]

该函数最小值是(f(x,y)=0)，且(x=0,y=0)

直接用偏导数可以计算出函数最小值，有前提条件，那就是该函数是凸函数。凸函数的定义：在函数上任意两点连接的线段总是在函数图上方或者重合

局部最优解与全局最优解

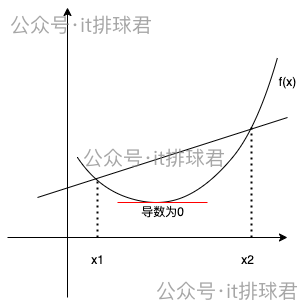
如果函数不是凸函数，而是类似于这种，在某一个定义域内是凸函数

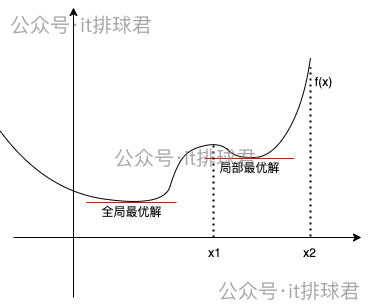
使用坐标下降法的时候，选择的初始值如果在((x1,x2))之间，那找到的最小值就是局部最小，而非全局最小。之前介绍的梯度下降法也有同样的问题

那要怎么解决这个问题呢？不好意思，我也不会，还没学习到，所以暂时略过，后面再说 -_- !

lasso回归

介绍完坐标下降法之后，最后来到了本文的主题，lasso回归，为什么lasso回归能够降低无用参数的影响？lasso回归就是添加了一个参数的绝对值之和作为惩罚项，用线性回归为例，线性回归的损失函数常用MSE

[text{MSE} = frac{1}{n} sum_{i=1}^{n} (y_i - hat{y}_i)^2 ]

lasso的数学表达：

[mathcal{L} = frac{1}{n} sum_{i=1}^{n} (y_i - hat{y}_i)^2 + lambda sum_{j=1}^{p} |β_j| ]

我们通过一个例子，来说明lasso回归的工作流程。有一个数学模型：2个特征分别为(x_1)、(x_2)，分别使用不带lasso惩罚项与带lasso惩罚项来进行推导

样本	(β_1)	(β_2)	y
1	1	1	2
2	2	1	2
3	3	2	4.5

最小二乘法

不带lasso惩罚项，就直接用最小二乘法求解，在之前的小结中曾经推倒过多元回归中最小二乘法的计算公式：

[β=(X^TX)^{-1}X^Ty_i ]

首先特征矩阵(X)：
$ X=
begin{pmatrix}
1 & 1
2 & 1
3 & 2
end{pmatrix}
$， (X)的转置
$ X^T=
begin{pmatrix}
1 & 2 & 3
1 & 1 & 2
end{pmatrix}
$

矩阵乘法，(X^T·X= begin{pmatrix} 1 & 2 & 3 \ 1 & 1 & 2 end{pmatrix} begin{pmatrix} 1 & 1 \ 2 & 1 \ 3 & 2 end{pmatrix} = begin{pmatrix} 14 & 9 \ 9 & 6 end{pmatrix} )

矩阵求逆常用初等变换法以及伴随矩阵法，对于上述演示数据，笨办法我直接用伴随矩阵求出来，但是都ai时代了，我决定使用chatgpt法（机智如我-_-） ：((X^TX)^{-1} = begin{pmatrix} 2 & -3 \ -3 & frac{14}{3} end{pmatrix} )

根据矩阵结合律，我先算一下后面：(X^T·y_i = begin{pmatrix} 1 & 2 & 3 \ 1 & 1 & 2 end{pmatrix} begin{pmatrix} 2 \ 3 \ 4.5 end{pmatrix} = begin{pmatrix} 21.5 \ 14 end{pmatrix} )

最终计算出系数 (beta =(X^TX)^{-1}X^Ty_i = begin{pmatrix} 2 & -3 \ -3 & frac{14}{3} end{pmatrix} begin{pmatrix} 21.5 \ 14 end{pmatrix} = begin{pmatrix} 1 \ frac{2.5}{3} end{pmatrix} approx begin{pmatrix} 1 \ 0.8333 end{pmatrix} )

最终，通过最小二乘法，拟合函数为

[y = x_1+0.8333x_2 ]

带lasso惩罚项

为了计算方便，先将公式简化，把n去掉，因为同时缩放n倍，对于结果比对没有影响

[mathcal{L} = frac{1}{n} sum_{i=1}^{n} (y_i - hat{y}_i)^2 + lambda sum_{j=1}^{p} |β_j| = sum_{i=1}^{n} (y_i - hat{y}_i)^2 + lambda sum_{j=1}^{p} |β_j| ]

lasso有一个超参数(lambda)，我们先设置一下(lambda = 2)，用坐标下降法：

1）首先寻找一个点(beta=(0,0))，计算出函数值

[begin{aligned} mathcal{L} &= sum_{i=1}^{n} (y_i - hat{y}_i)^2 + lambda sum_{j=1}^{p} |β_j| \ &= ((2-beta_1-beta_2)^2 + (3-2beta_1-beta_2)^2 + (4.5-3beta_1-2beta_2)^2 + (lambdasum_{j=1}^{p}|beta|)) \ &= 4+9+20.25 = 33.25 end{aligned} ]

2）先分别求偏导

[begin{aligned} frac {partial f}{partial beta_1} &= ((2-beta_1-beta_2)^2 + (3-2beta_1-beta_2)^2 + (4.5-3beta_1-2beta_2)^2 + (lambdasum_{j=1}^{p}|beta|))' \ &= 28beta_1+18beta_2-43 + (lambdasum_{j=1}^{p}|beta|)' end{aligned} ]

这里的惩罚项并没有进行导数计算，原因一会再说，先记为(f_{absolute}'=(lambdasum_{j=1}^{p}|beta|)')

所以最终对(beta_1)求偏导：

[frac {partial f}{partial beta_1} = 28beta_1+18beta_2-43 + f_{absolute}' ]

同理对(beta_2)求偏导：

[frac {partial f}{partial beta_2} = 18beta_1+12beta_2-28 + f_{absolute}' ]

由于绝对值在0处不可导，所以绝对值的导数需要分段来研究

[frac{partial f_{absolute}}{beta_i} = lambda(|beta_i|)' = left{ begin{array}{ll} lambda·beta_i qquad ,beta_i>0 \ 0 qquad ,beta_i=0 \ -lambda·beta_i qquad ,beta_i

3）第一次迭代，(beta=(0,0))，更新(beta_1)，固定(beta_2=0)

[begin{aligned} frac {partial f}{partial beta_1} &= 28beta_1+18beta_2-43 + f_{absolute}' = 28beta_1 - 43 + lambda(|beta_i|)' \ &= left{ begin{array}{ll} 28beta_1-43+2 qquad ,beta_1>0 \ 28beta_1-43 qquad ,beta_1=0 \ 28beta_1-43-2 qquad ,beta_1

令偏导数为0

[begin{aligned} beta_1 = left{ begin{array}{ll} frac{41}{28} approx 1.464 qquad ,beta_1>0 \ frac{43}{28} qquad ,beta_1=0 \ frac{45}{28} approx 1.607 qquad ,beta_1

由于(beta_1与计算结果矛盾，所以(beta_1=1.464)

4）第一次迭代，固定(beta_1=1.464)，更新(beta_2)

[begin{aligned} frac {partial f}{partial beta_2} &= 18beta_1+12beta_2-28 + f_{absolute} = 12beta_2-28 + lambda(|beta_i|)' \ &= left{ begin{array}{ll} 26.352+12beta_2-28+2 qquad ,beta_2>0 \ 26.352+12beta_2-28 qquad ,beta_2=0 \ 26.352+12beta_2-28-2 qquad ,beta_2

令偏导数为0

[begin{aligned} beta_2 = left{ begin{array}{ll} frac{-0.352}{12} approx -0.0293 qquad ,beta_2>0 \ frac{1.648}{12} approx 0.1373 qquad ,beta_2=0 \ frac{3.648}{12} = 0.304 qquad ,beta_2

这个。。。。怎么全是矛盾的？？计算出来的(beta_2)都不对，那(beta_2)到底取值是什么，这里要用次梯度来解决这个问题，一会再详细讨论，这里只需要知道，(beta_2)取值在[-0.0293, 0.304]之间，而最优解就是0

5）计算函数值

[begin{aligned} mathcal{L}(1.464, 0) &= sum_{i=1}^{n} (y_i - hat{y}_i)^2 + lambda sum_{j=1}^{p} |β_j| \ &= ((2-beta_1-beta_2)^2 + (3-2beta_1-beta_2)^2 + (4.5-3beta_1-2beta_2)^2 + (lambdasum_{j=1}^{p}|beta|)) \ &approx 0.2872+0.0582+0.2446+2.928 = 3.518 end{aligned} ]

6）第一轮小结

• 函数最小值(mathcal{L}(x,y)=3.518)，从33.25下降而来
• (|Δbeta_1|=|0-1.464| approx 1.464)
• (|Δbeta_2|=|0-0| = 0)

第一次迭代就已经把(beta_2)给家人们打下来了，(beta_2)对于寻找函数最小值，已经没有意义了，换句话来说，该特征对于提升模型性能意义不大

但是依然需要继续寻找最合适的(beta_1)，直至收敛，所以还需要继续迭代下去，下面就不演示了

继续迭代。。。。最终经过lasso回归的拟合函数应该是这样的：

[y=beta_1x_1 ]

可以看到，lasso回归有可能把一些特征的系数压缩成0了，从而去掉该特征对于目标函数的影响，从而降低该特征的影响，提高了模型了泛化能力

次梯度

在刚才的推导中，遇到了这个问题，( begin{aligned} beta_2 = left{ begin{array}{ll} frac{-0.352}{12} approx -0.0293 qquad ,beta_2>0 \ frac{1.648}{12} approx 0.1373 qquad ,beta_2=0 \ frac{3.648}{12} = 0.304 qquad ,beta_2，(beta_2)与所有的结果都是矛盾的，之所以会出现这种情况，是由于对绝对值求导数导致的。我们都知道，绝对值在0的时候是不可导的

当(beta=0)的时候，需要使用次梯度的概念，什么是次梯度，我这里也不班门弄斧的搬概念了，大家有兴趣自己去google一下

这里只需要记住次梯度是一个集合，它的范围就是，若( begin{aligned} beta_2 = left{ begin{array}{ll} a qquad ,beta_2>0 \ b qquad ,beta_2，那(beta=0)的次梯度是([a,b])之间

更直接一点，如果我们在次梯度集合中，找到为0的选项，那就意味着找到了函数的最小值点

这也说明了，lasso回归不能直接用导数为0的方法来找最优解，需要用到坐标下降法的原因

小结

笔者写这篇文章的时候真是头皮发麻，“凸函数”、“最优解”等名词让我回想起学生时代被高数、微积分支配的恐惧，如今再次面对，竟然能够坦然处之，甚至觉得莫名亲切，进而会心一笑。被动接受与主动求索，还真是不一样

联系我

• 联系我，做深入的交流
  

---

至此，本文结束
在下才疏学浅，有撒汤漏水的，请各位不吝赐教...