[f'(x) = frac{partial y}{partial x} = lim_{Delta x to 0} frac{f(x + Delta x) - f(x)}{Delta x} = a ]

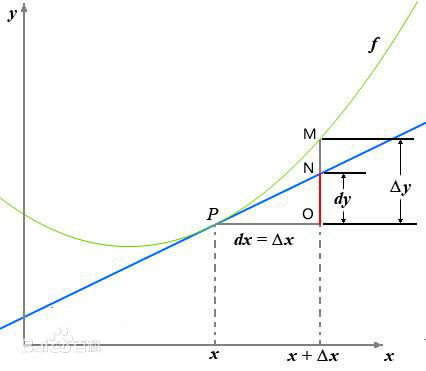
（该图来自于百度百科）

偏导数

偏导数与导数的本质是一样的，只不过偏导数解决的是多变量的问题

[frac{partial f}{partial x_i} = lim_{Delta x_i to 0} frac{f(x_1, dots, x_i + Delta x_i, dots, x_n) - f(x_1, dots, x_i, dots, x_n)}{Delta x_i} ]

比如二元函数(f(x,y))

对(x)求偏导：

[frac{partial f}{partial x} = lim_{Delta x to 0} frac{f(x + Delta x, y) - f(x, y)}{Delta x} ]

对(y)求偏导：

[frac{partial f}{partial y} = lim_{Delta y to 0} frac{f(x, y + Delta y) - f(x, y)}{Delta y} ]

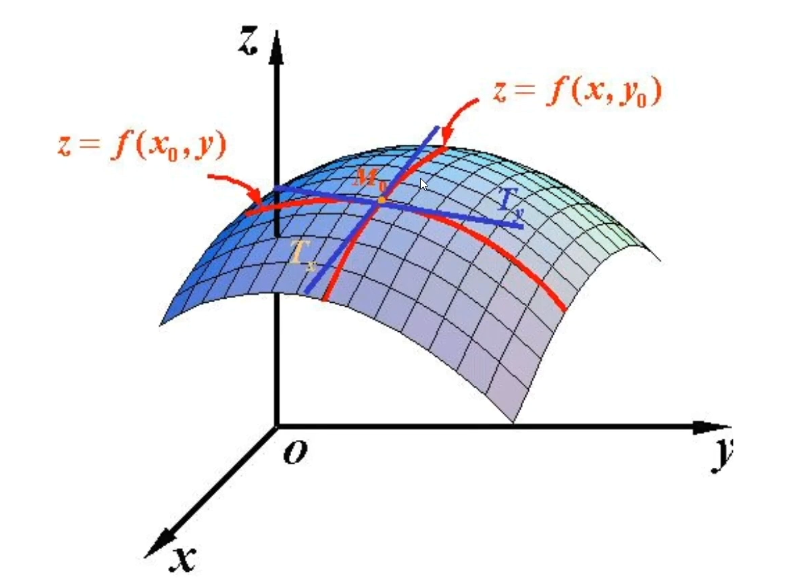
（该图来自于百度百科）

超过二元的就画不出来图来了

方向导数

导数与偏导数都是自变量相对于某一轴方向（比如x相对于x轴，y相对于y轴）讨论变化率，而方向导数讨论的则是，自变量可以在其定义域内自由选择方向

一个多元函数(f)和一个方向向量(u)，方向导数(D_uf)表示函数(f)在(u)方向的变化率

[D_{mathbf{u}}f(a) = lim_{h to 0} frac{f(a + hu) - f(a)}{h} ]

用二元函数举例：

[D_{mathbf{u}}f(x_0, y_0) = lim_{h to 0} frac{f(x_0 + h u_1, y_0 + h u_2) - f(x_0, y_0)}{h} ]

• (u_1 u_2)表示方向(u = (u1, u2))
• h表示沿着(u)方向的位移

梯度

梯度是多元函数在某一点处所有偏导数构成的向量，表示函数在该点处变化最快的方向及其变化率，对于(f(x_1,x_2,...,x_n))，其梯度记为(nabla f)

[nabla f = left(frac{partial f}{partial x_1}, frac{partial f}{partial x_2}, dots, frac{partial f}{partial x_n}right) ]

• 方向：梯度指向函数在该点增长最快的方向
• 大小：梯度的模表示函数在该方向上的最大变化率

方向导数：梯度与单位方向向量u的点积

[D_uf=nabla f⋅u ]

当(u)与(nabla f)同方向时，方向导数最大
当(u)与(nabla f)反方向时，方向导数最小

小结

梯度与方向导数：梯度是方向导数中变化率最大的那一个：梯度的方向是方向导数取最大值的方向，而梯度的模长（大小）等于该最大方向导数的值
方向导数与偏导数：偏导数是方向导数的特例，即(u=(0,1))，简而言之，方向导数在坐标轴上移动，就是偏导数

了解了梯度的诞生以及概念之后，终于可以来讨论一下本文的主题：梯度下降法

梯度下降法

在回归任务中，用于评估模型的重要指标是损失函数MSE，提高模型的泛化能力就是设法降低MSE

上述关于梯度的描述，梯度就是函数变化率最快的方向，那梯度下降法就是不断沿着付梯度方向寻找MSE的最小值。不同于最小二乘法只能用于线性模型，梯度下降法适用于大部分模型，包括线性回归、逻辑回归等等

核心思想

• 函数的梯度指向函数值增长最快的方向，负梯度方向则是函数值下降最快的方向
• 通过不断沿负梯度方向调整参数，逐步逼近函数的最小值点

步骤

• 初始化，随机选择初始参数或者全部设置为0
• 迭代更新，每迭代一次都会更新参数的值：$$theta_{t+1}=theta_t - eta ⋅ nabla f(theta_t)$$
  • (theta_t)：第(t)次迭代的参数值
  • (eta)：每次更新的幅度，也叫学习率
  • (nabla J(theta_t))：目标函数(f)在(theta_t)的梯度
• 终止迭代的条件：
  • 梯度很小：梯度的模长很小，一般小于(10^{-6})
  • 损失函数变化很小：一般小于(10^{-6})
  • 到达最大迭代次数

计算过程

我们用本系列的第一节：一元线性回归中的数据，用梯度下降法详细演示一次

data = {
    'result': [0.63, 0.72, 0.72, 0.63, 0.57, 0.52, 0.48, 0.47],
    'feature1': [22.48, 19.50, 18.02, 16.97, 15.78, 15.11, 14.02, 13.24]
}

目标是找到一组参数，使得损失函数MSE最小：

[text{MSE} = frac{1}{n} sum_{i=1}^{n} (y_i - hat {y}_i)^2 ]

带入(y=beta_0 + beta_1 x)

[f(beta_0 , beta_1) = frac{1}{n} sum_{i=1}^{n} (beta_0 + beta_1 x_i - hat {y}_i)^2 ]

首先计算梯度，分别对(beta_0)、(beta_1)求偏导

先对(beta_0)求偏导：

[frac{partial f}{partial β_0} = frac{1}{n} sum_{i=1}^{n} 2(β_0 + β_1x_i - hat {y}_i)⋅(β_0 + β_1x_i - hat {y}_i)' = frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i) ]

在对(beta_1)求偏导：

[frac{partial f}{partial β_1} = frac{1}{n} sum_{i=1}^{n} 2(β_0 + β_1x_i - hat {y}_i)⋅(β_0 + β_1x_i - hat {y}_i)' = frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i)⋅x_i ]

至此得出梯度：

[nabla f = (frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i), frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i)⋅x_i) ]

设置参数，学习率(eta=0.001)，迭代次数100次，开始迭代：

1）第一轮迭代，先初始化(beta_0) (beta_1)为0

计算损失函数：

[begin{aligned} MSE &= f(beta_0 , beta_1) = frac{1}{n} sum_{i=1}^{n} (beta_0 + beta_1 x_i - hat {y}_i)^2 \ &= frac{1}{8}[(0-0.63)^2+(0-0.72)^2+...+(0-0.47)^2] = 0.35965 end{aligned} ]

计算梯度：

[begin{aligned} frac{partial f}{partial β_0} &= frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i) \ &= frac{1}{4}[(0-0.63)+(0-0.72)+...+(0-0.47)] = -1.185 end{aligned} ]

[begin{aligned} frac{partial f}{partial β_1} &= frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i)⋅x_i \ &= frac{1}{4}[(0-0.63)·22.48+(0-0.72)·19.50+...+(0-0.47)·13.24] = -20.418025 end{aligned} ]

[nabla f = (-1.185, -20.418025) ]

损失函数与梯度均小于(10^{-6})，继续迭代第二轮

2）第二轮迭代，先初始化(beta_0) (beta_1)

[beta_0 ← beta_0 - eta · frac{partial f}{partial β_0} = 0 - 0.001·(-1.185) = 0.001185 ]

[beta_1 ← beta_1 - eta · frac{partial f}{partial β_1} = 0 - 0.001·(-20.418025) = 0.020418025 ]

计算损失函数：

[MSE = f(beta_0 , beta_1) = frac{1}{n} sum_{i=1}^{n} (beta_0 + beta_1 x_i - hat {y}_i)^2 = 0.064501 \ ]

计算梯度：

[frac{partial f}{partial β_0} = frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i) = -0.492909 ]

[frac{partial f}{partial β_1} = frac{2}{n} sum_{i=1}^{n} (β_0 + β_1x_i - hat {y}_i)⋅x_i = -8.395268 ]

[nabla f = (-0.492909, -8.395268) ]

损失函数与梯度均小于(10^{-6})，继续迭代第三轮...

就这样不断迭代下去，直至满足停止的条件，停止之后，该轮次的(β_0) (β_1)就是最佳参数

联系我

• 联系我，做深入的交流

---

至此，本文结束
在下才疏学浅，有撒汤漏水的，请各位不吝赐教...