在运维职业生涯中,qps是一个绕不开的话题,leader经常在问,我们的qps是多少,系统能不能抗住啊???老板在问,我们的qps是多少,有没有降本的空间啊???面试的时候,面试官问,你们的qps是多少啊。。。。
如果我能预测qps与系统压力之间的关系,那一定很不错吧?关于leader,我们的qps是100w,系统完全能够扛得住;关于老板,我们的qps是1000w,系统经过优化之后,依然可以降本20%;关于面试官,我们的qps是1亿,并且系统 完全没有问题
为了在能够吹牛逼的情况下,把当前的工作(系统稳定,探索系统极限)做好,所以有必要搞一搞
机器学习中,一元线性回归是较为简单的算法,并且特征只需要一个,就可以预测结果,我们就用它来开始学习,由于系统压力有很多指标,cpu、内存、io、带宽等等等等,为了简化,我们就选cpu作为压力的代表,详细讨论一下,qps与cpu的变化特征
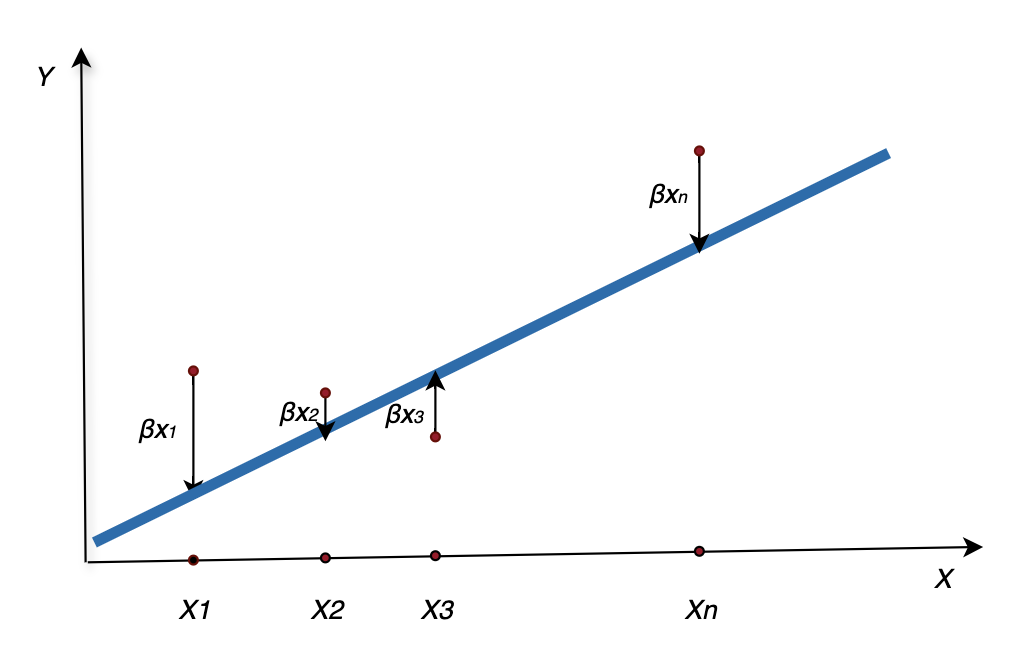
一元线性回归,就是分析自变量与因变量之间的线性关系,由于自变量只有1个,那线性关系就会容易得多,就是一次函数。简而言之,寻找一条直线,最大程度地去拟合样本特征(qps)和样本(cpu)输出标记之间的关系
我们先来看一看怎么使用一元线性回归
先不管什么鸡r原理,我目前也不想懂,我就需要看到效果,怎么进行一元回归分析。好的,请使用使用scikit-learn包,帮助我们快速上手
安装
pip3 install -U scikit-learn
使用
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import pandas as pd
# 准备数据
data = {
'result': [0.63, 0.72, 0.72, 0.63, 0.57, 0.52, 0.48, 0.47],
'feature1': [22.48, 19.50, 18.02, 16.97, 15.78, 15.11, 14.02, 13.24]
}
df = pd.DataFrame(data)
X = df[['feature1']]
y = df['result']
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建模型并训练
model = LinearRegression()
model.fit(X_train, y_train)
# 模型评估
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"MSE: {mse}, R²: {r2}")
# 预测
new_data = pd.DataFrame({
"feature1": [10.53, 20.81]
})
predicted_result = model.predict(new_data)
print("预测的 result:", predicted_result)
脚本!启动:

简单解读:这个模型不行!
好的,综上所述,本例造成模型不行的原因,就是数据量不够
下面介绍两个重要的概念
拟合:模型能够解释训练数据的程度
泛化:指模型在未知数据上的表现能力。一个好的模型不仅要在训练数据上表现良好,还要能够对未见过的数据做出准确的预测
在上一小节,我们训练的模型属于欠拟合,并且泛化能力弱
一元线性回归就是在一堆有规律的散列点当中,找到一条能够解释这些散列点的线
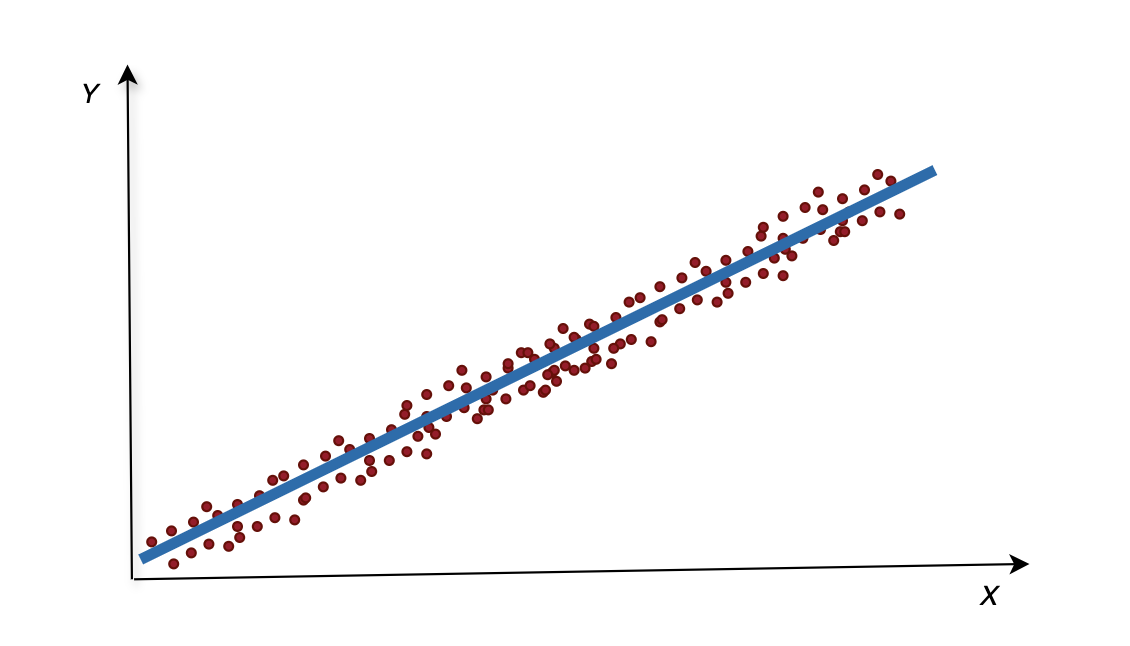
scikit-learn包的默认算法线性回归通常使用均方误差(MSE)来作为损失函数,衡量测试值与真实值之间的差异
[text{MSE} = frac{1}{n} sum_{i=1}^{n} (y_i - hat{y}_i)^2 ]
其中(y_i)是真实值,(hat{y}_i)是预测值
正如前文提到,MSE中真实值与预测值,有平方计算,那就会放大误差,所以MSE可以非常有效的检测误差项
下面我们来详细解释一下最小二乘法的原理,最小二乘法的核心思想是找到一组参数,使得模型预测值与实际观测值之间的误差平方和最小。细心的各位看这个定义,就发现这不就是上面的MSE的定义吗?只不过区别就是MSE取了样本平均值
[text{L} = sum_{i=1}^{n} (y_i - hat{y}_i)^2 ]
其中(y_i)是真实值,(hat{y}_i)是预测值
这里来八卦一下最小二乘法。该算法是由法国大佬勒让德提出来的,误差是没有办法避免的,但是通过最小二乘法,使误差平方和达到最小,在各方程的误差之间建立了一种平衡,而这有助于揭示系统的更接近真实的状态。后面由高斯大佬证明了,误差服从了标准正态分布。所以误差平方就成为了在回归分析中计算误差的最佳准则
用于评估线性回归模型拟合优度的重要指标,其取值范围为 [0, 1]
[R^2 = 1 - frac{sum_{i=1}^{n} (y_i - hat{y}_i)^2}{sum_{i=1}^{n} (y_i - bar{y})^2} ]
其中(y_i)是真实值,(hat{y}_i)是预测值,(bar{y})是均值
scikit-learn中的常用参数test_size:是用于划分数据集的关键参数,用于指定测试集的比例或大小,常见的值为 0.2 或 0.3random_state:用于控制随机过程的随机性
至此,本文结束
在下才疏学浅,有撒汤漏水的,请各位不吝赐教...
本文来自博客园,作者:it排球君,转载请注明原文链接:https://www.cnblogs.com/MrVolleyball/p/19031555
 登录查看全部
登录查看全部
参与评论
手机查看
返回顶部