
当你踏入数据分析的大门时,可能会被海量的数据淹没,感到无从下手。
想象一下,你想了解一座巨大森林里所有树木的平均高度,难道要一棵一棵地去测量吗?这显然不现实。
这时,“抽样” 这个强大的工具就该登场了!
本文将带你全面了解各种抽样方法,并用Python代码演示实际应用。
抽样 是从总体中选取部分样本进行分析的过程。
这样做的主要原因是:
在抽样的世界里,主要有两种不同的理念,形成了两大阵营:
接下来,我们将重点介绍几种主流的抽样方法。
非随机抽样虽然在严谨的数据分析中需要谨慎使用,但在某些场景下依然有其价值。
它的实现原理是:根据研究者的主观判断、方便程度或特定需求来选择样本,不保证每个个体都有被抽中的机会。
常见的非随机抽样包括方便抽样、判断抽样、滚雪球抽样等。
典型的应用场景有:
下面用Python实现一个简单的非随机抽样的示例。
import pandas as pd
import numpy as np
# 模拟创建一个包含1000名用户的数据集
np.random.seed(42)
data = {
'user_id': range(1, 1001),
'age': np.random.randint(18, 60, size=1000),
'city': np.random.choice(['北京', '上海', '广州', '深圳', '杭州'], size=1000),
'activity_score': np.random.randint(1, 101, size=1000) # 活跃度评分,1-100
}
df = pd.DataFrame(data)
# 非随机抽样:判断抽样
# 我们主观判断活跃度分数高于90的用户为高活跃度代表
high_activity_sample = df[df['activity_score'] > 90]
print("判断抽样(活跃度>90)的样本量:", len(high_activity_sample))
print(high_activity_sample.head())
运行结果:
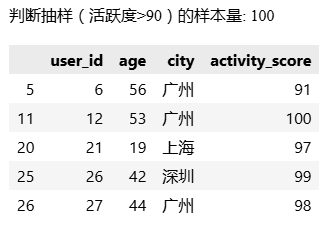
随机抽样是数据分析的基石,它能确保样本的代表性,从而让我们的分析结论更具说服力。
随机抽样一般有下面四种方式:
这是最基础的随机抽样方法,确保总体中每个个体被抽中的概率完全相等。
就像从一个装满小球的箱子里随机摸球一样,每个球被摸到的机会都是一样的。
它的典型应用场景有:
下面是Python实现的一个简单随机抽样示例。
先创建测试数据,这些数据在后面其他随机抽样示例中也会使用。
# 创建模拟数据集:某公司客户数据
np.random.seed(42) # 设置随机种子保证结果可重现
customer_data = pd.DataFrame({
'customer_id': range(1, 1001),
'age': np.random.randint(18, 70, 1000),
'income': np.random.normal(50000, 15000, 1000).astype(int),
'satisfaction_score': np.random.randint(1, 11, 1000)
})
print("原始数据集概况:")
print(f"数据量:{len(customer_data)}")
print(f"平均收入:{customer_data['income'].mean():.2f}")
print(f"平均满意度:{customer_data['satisfaction_score'].mean():.2f}")
# 运行结果:
'''
原始数据集概况:
数据量:1000
平均收入:50863.12
平均满意度:5.39
'''
然后进行简单随机抽样:
# 简单随机抽样
simple_random_sample = customer_data.sample(n=50, random_state=42)
print("简单随机抽样结果:")
print(f"样本量:{len(simple_random_sample)}")
print(f"样本平均收入:{simple_random_sample['income'].mean():.2f}")
print(f"样本平均满意度:{simple_random_sample['satisfaction_score'].mean():.2f}")
# 运行结果:
'''
简单随机抽样结果:
样本量:50
样本平均收入:48647.12
样本平均满意度:4.76
'''
抽样数据与总体数据相比,收入分布和满意度分布情况如下:
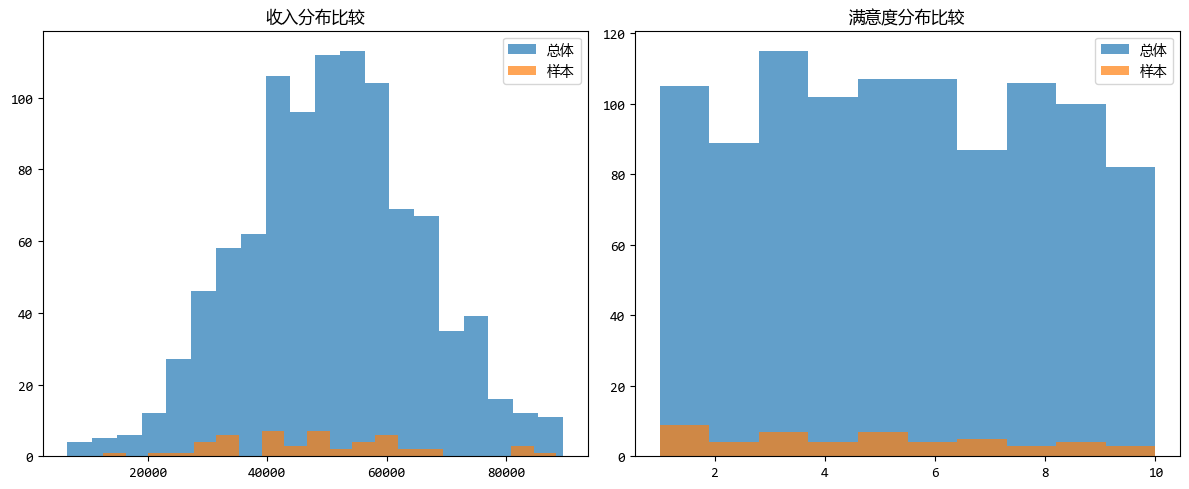
分层随机抽样是先将总体按照某种特征分成若干个互不重叠的“层”,然后在每个层内部分别进行简单随机抽样。
这种方法可以保证样本的结构与总体的结构相似,特别适用于总体内部差异较大的情况。
它的典型应用场景有:
下面是Python实现的一个分层随机抽样示例。
# 创建分层:按年龄分组
customer_data["age_group"] = pd.cut(
customer_data["age"],
bins=[0, 30, 45, 60, 100],
labels=["青年", "中青年", "中年", "中老年"],
)
print("各年龄组人数:")
print(customer_data["age_group"].value_counts())
# 分层随机抽样:每层按比例抽取
stratified_sample = (
customer_data.groupby("age_group", observed=False)
.apply(
lambda x: x.sample(frac=0.05, random_state=42),
include_groups=False,
)
.reset_index()
)
print("n分层随机抽样结果:")
print(f"样本量:{len(stratified_sample)}")
print("样本中各年龄组分布:")
print(stratified_sample["age_group"].value_counts())
# 运行结果:
'''
各年龄组人数:
age_group
中青年 297
中年 282
青年 238
中老年 183
Name: count, dtype: int64
分层随机抽样结果:
样本量:50
样本中各年龄组分布:
age_group
中青年 15
中年 14
青年 12
中老年 9
Name: count, dtype: int64
'''
分层随机抽样和简单随机抽样,以及总体数据对于平均收入的估计如下:
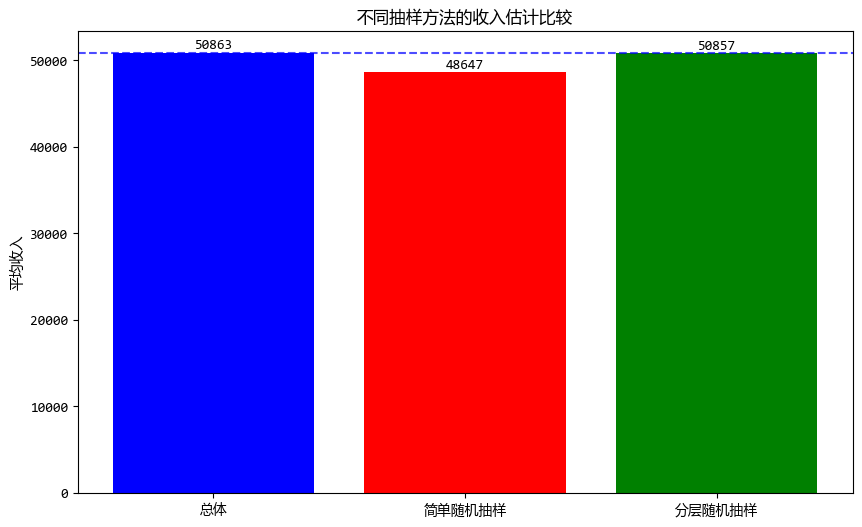
从图中可以看出,分层随机抽样更接近于总体的值。
系统随机抽样是将总体中的所有单位按一定顺序排列,然后按照固定的间隔(步长)来抽取样本。
比如,从1000人中抽取100人,可以每隔10人抽取1人。
它的典型应用场景有:
下面是Python实现的一个系统随机抽样示例。
# 系统随机抽样
def systematic_sampling(data, step):
start = np.random.randint(0, step)
indices = range(start, len(data), step)
return data.iloc[indices]
systematic_sample = systematic_sampling(customer_data, 20) # 每20个抽1个
print("系统随机抽样结果:")
print(f"样本量:{len(systematic_sample)}")
print(f"样本平均收入:{systematic_sample['income'].mean():.2f}")
# 运行结果:
'''
系统随机抽样结果:
样本量:50
样本平均收入:50763.34
'''
系统随机抽样的示意图如下:
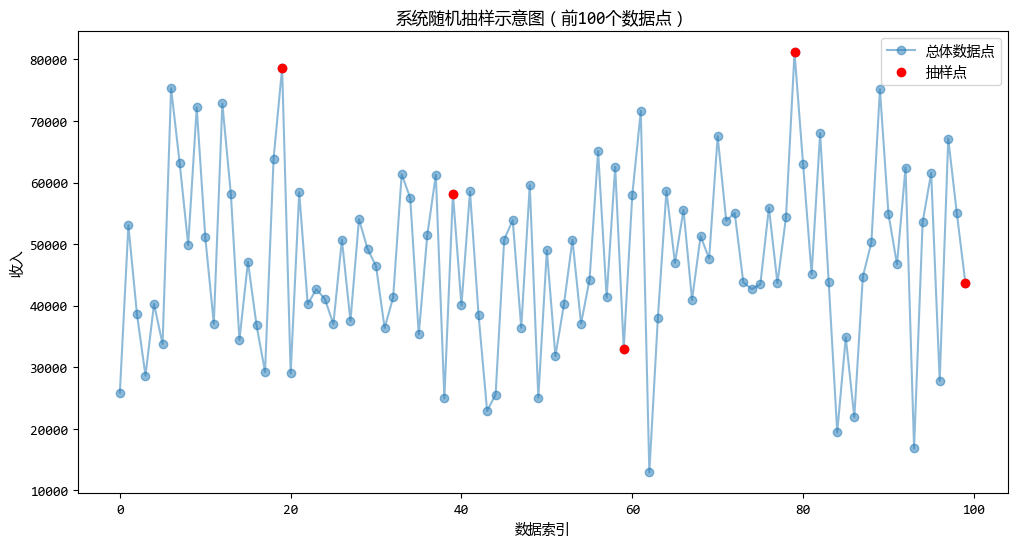
整群随机抽样是将总体划分为若干个互不重叠的“群”,然后随机抽取其中的若干个群,对抽中的群里的所有单位进行调查。
它的典型应用场景是:
下面是Python实现的一个整群随机抽样示例。
# 创建模拟的群组数据:假设客户按地区分组
regions = ['北京', '上海', '广州', '深圳', '杭州', '成都', '武汉', '西安']
customer_data['region'] = np.random.choice(regions, len(customer_data))
print("各地区客户数量:")
print(customer_data['region'].value_counts())
# 整群随机抽样:随机选择3个地区,调查这些地区的所有客户
selected_regions = np.random.choice(regions, size=3, replace=False)
cluster_sample = customer_data[customer_data['region'].isin(selected_regions)]
print(f"n抽中的地区:{selected_regions}")
print("整群随机抽样结果:")
print(f"样本量:{len(cluster_sample)}")
print(f"样本平均收入:{cluster_sample['income'].mean():.2f}")
print(f"总体平均收入:{customer_data['income'].mean():.2f}")
# 运行结果:
'''
各地区客户数量:
region
武汉 141
广州 133
成都 132
杭州 124
北京 120
上海 118
深圳 116
西安 116
Name: count, dtype: int64
抽中的地区:['杭州' '深圳' '武汉']
整群随机抽样结果:
样本量:381
样本平均收入:50319.75
总体平均收入:50863.12
'''
整群随机抽样得到的平均收入与总体数据的比较如下图:它们的值非常接近。
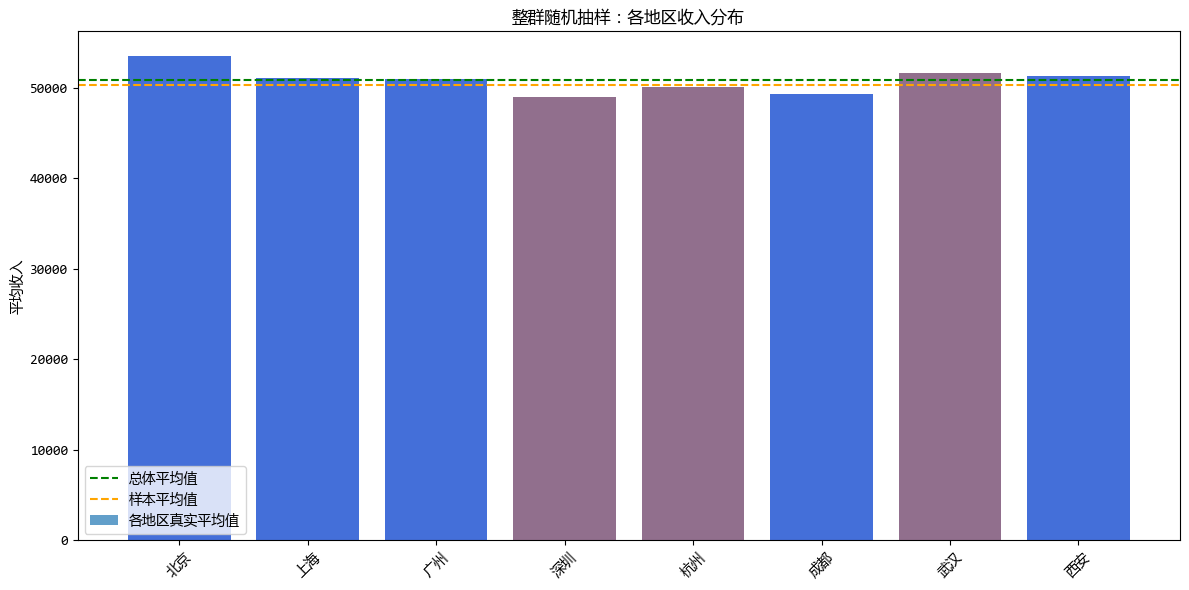
为了更直观地感受不同抽样方法带来的差异,我们从同一个数据集中,使用不同的方法抽取大约相同规模的样本,来比较各种抽样方法。
# 创建更复杂的数据集来演示各种抽样方法
np.random.seed(42)
company_data = pd.DataFrame(
{
"employee_id": range(1, 1001),
"department": np.random.choice(
["技术", "销售", "市场", "人事", "财务"],
1000,
p=[0.3, 0.25, 0.2, 0.15, 0.1],
),
"salary": np.random.normal(80000, 20000, 1000).astype(int),
"experience": np.random.exponential(5, 1000).astype(int) + 1,
}
)
# 修正可能的负工资
company_data["salary"] = company_data["salary"].clip(lower=30000)
print("公司员工数据概况:")
print(f"总员工数:{len(company_data)}")
print(f"平均工资:{company_data['salary'].mean():.2f}")
print("n各部门人数:")
print(company_data["department"].value_counts())
# 应用不同抽样方法
samples = {
"简单随机抽样": company_data.sample(n=100, random_state=42),
"分层随机抽样": company_data.groupby("department")
.apply(lambda x: x.sample(frac=0.1, random_state=42), include_groups=False)
.reset_index(),
"系统随机抽样": systematic_sampling(company_data, 10),
"整群随机抽样": company_data[
company_data["department"].isin(
np.random.choice(company_data["department"].unique(), 2, replace=False)
)
],
}
# 比较结果
comparison = pd.DataFrame(
{
"方法": ["总体"] + list(samples.keys()),
"样本量": [len(company_data)] + [len(sample) for sample in samples.values()],
"平均工资": [company_data["salary"].mean()]
+ [sample["salary"].mean() for sample in samples.values()],
"工资误差": [0]
+ [
abs(sample["salary"].mean() - company_data["salary"].mean())
for sample in samples.values()
],
}
)
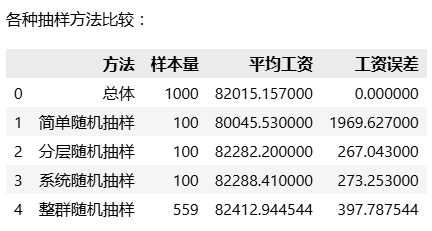
print("n各种抽样方法比较:")
print(comparison)
# 运行结果:
'''
公司员工数据概况:
总员工数:1000
平均工资:82015.16
各部门人数:
department
技术 319
销售 240
市场 198
人事 143
财务 100
Name: count, dtype: int64
'''
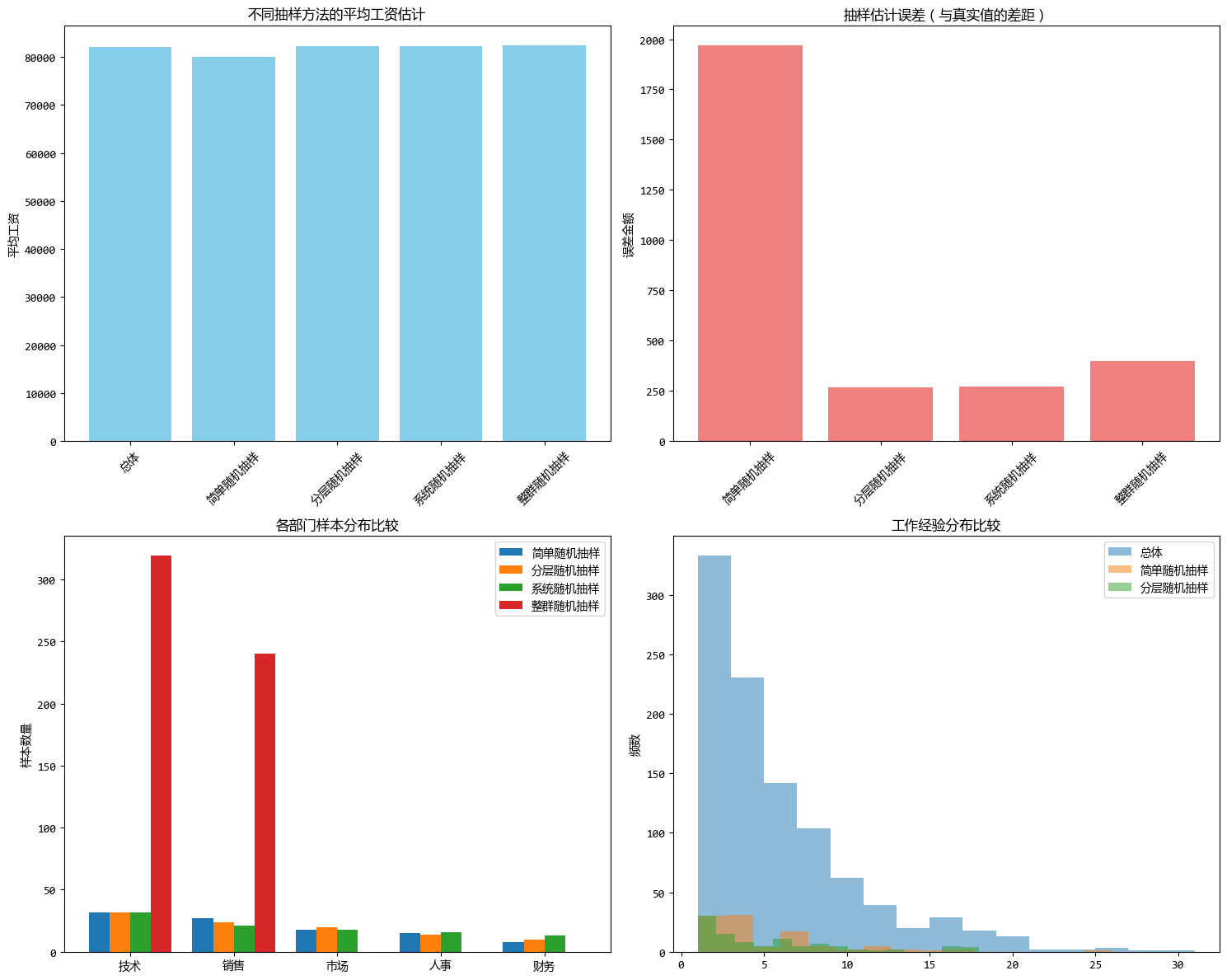
本文介绍了常用的抽样方法,并给出了各种抽样方法的典型应用场景以及Python代码实现方式。
重点是四种随机抽样的方法,选择抽样方法时需要考虑:
记住,没有 "最好" 的抽样方法,只有 "最合适" 的。
在实际工作中,要根据具体情况灵活选择和组合使用不同的抽样方法。
 登录查看全部
登录查看全部
参与评论
手机查看
返回顶部